Néron model
In algebraic geometry, a Néron model (or Néron minimal model, or minimal model) for an abelian variety AK defined over a local field K is the "best possible" group scheme AO defined over the ring of integers R of the local field K that becomes isomorphic to AK after base change from R to K.
They were introduced by André Néron (1964).
Definition
Suppose that R is a Dedekind domain with field of fractions K, and suppose that AK is an abelian variety over K. Then a Néron model is defined to be a universal separated smooth scheme AR over R with a rational map to AK. More precisely, this means that AR is a separated smooth scheme over R with general fiber AK, such that any rational map from a smooth scheme over R to AR can be extended to a unique morphism (Néron mapping property). In particular, the canonical map 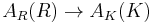 is a group isomorphism.
is a group isomorphism.
Néron models exist and are unique (up to unique isomorphism) and are commutative quasi-projective group schemes over R. The fiber of a Néron model over a closed point of Spec(R) is a smooth commutative algebraic group, but needs not be an abelian variety: for example, it may be disconnected, or unipotent, or a torus. Néron models exist as well for certain commutative groups other than abelian varieties, e.g., tori, but these are only locally of finite type. Néron models does not exist for the additive group.
Properties
- The formation of Néron models commutes with products.
- The formation of Néron models commutes with étale base change.
- An Abelian scheme A/S is the Néron model of its generic fibre.
References
- Artin, Michael (1986), "Néron models", in Cornell, G.; Silverman, Joseph H., Arithmetic geometry (Storrs, Conn., 1984), Berlin, New York: Springer-Verlag, pp. 213–230, MR861977
- Bosch, Siegfried; Lütkebohmert, Werner; Raynaud, Michel (1990), Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 21, Berlin, New York: Springer-Verlag, ISBN 978-3-540-50587-7, MR1045822
- I.V. Dolgachev (2001), "Néron model", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=N/n066290
- Néron, André (1964), "Modèles minimaux des variétes abèliennes sur les corps locaux et globaux", Publications Mathématiques de l'IHÉS 21: 5–128, doi:10.1007/BF02684271, MR0179172, http://www.numdam.org/item?id=PMIHES_1964__21__5_0
- W. Stein, What are Néron models? (2003)